偏微分方程接口

系数形式

全称：Coefficient Form PDE，简称：c

方程：

$$\{\begin{array}{llc}& e_a\frac{{\partial }^{2}u}{\partial t^2}+d_a\frac{\partial u}{\partial t}+\nabla \cdot (-c\nabla u-\alpha u+\gamma )+\beta \cdot \nabla u+au=f,& \mathrm{in}\Omega \\ & -\mathbf{n}\cdot (c\nabla u+\alpha u-\gamma )=g-qu+h^T\mu ,& \mathrm{on}\partial \Omega \\ & 0=R,& \mathrm{on}\partial {\Omega }_c\\ & u=r,& \mathrm{on}\partial {\Omega }_d\end{array}$$

其中，$\Omega$ 表示计算域（computational domain），$\partial \Omega$ 表示边界（domain boundary）

• 第二行为自然边界条件（natural boundary condition），不直接限制解空间
• 第三、第四行为基本边界条件（essential boundary condition），直接限制解空间

第二行 $-\mathbf{n}\cdot (c\nabla u+\alpha u-\gamma )=g-qu+h^T\mu$ 的含义详见 COMSOL

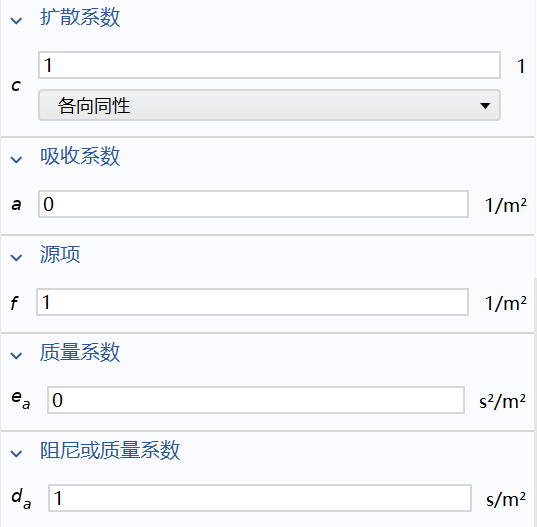
系数含义：

• $e_a$：质量，mass
• $d_a$：阻尼，damping
• $c$：扩散，diffusion
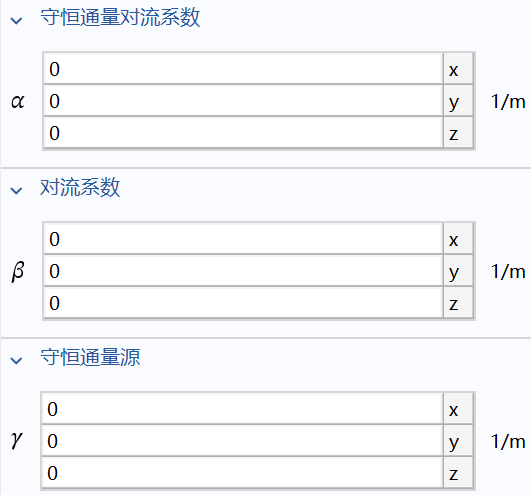
• $\alpha$：对流，convection，矢量
• $\gamma$：源，source，矢量
• $\beta$：对流，convection，矢量
• $a$：反应/吸收，absorption
• $f$：源，source

其中，$-c\nabla u-\alpha u+\gamma$ 为守恒通量，conservative flux

• $c$为标量时，表示各向同性扩散
• $c$为张量时，表示各向异性扩散，$c=\left(\begin{array}{ccc}{c}_{11}& c_{12}& c_{13}\\ c_{21}& c_{22}& c_{23}\\ c_{31}& c_{32}& c_{33}\end{array}\right)$
  • $c_{ij}$ 表示在 $x_j$ 方向上的浓度扩散，对 $x_i$ 方向上的扩散通量产生的影响

零通量：$-\mathbf{n}\cdot (c\nabla u+\alpha u-\gamma )=g-qu+h^T\mu =0$

狄利克雷边界条件：$\mathrm{on}\partial {\Omega }_d$，$u=r=?$，在指定边界上直接设置 $u$ 的值

• Dirichlet Boundary Condition

约束：$\mathrm{on}\partial {\Omega }_c$，$R=?=0$，在指定边界上强制某个表达式 $R$ 等于零

• Constraint

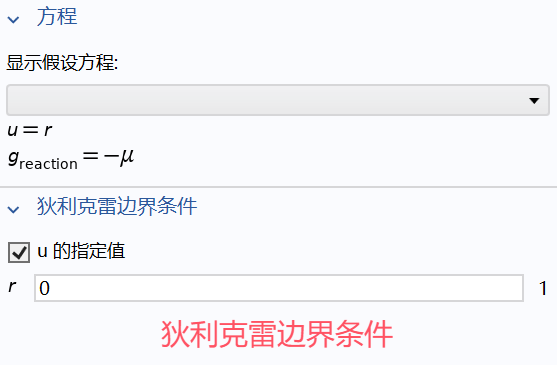
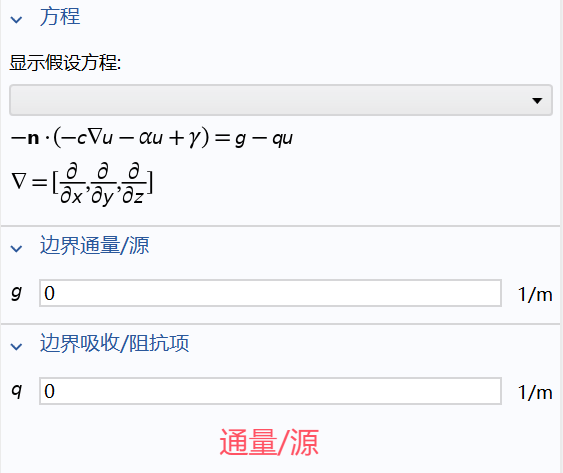
图中 $g_{\mathrm{reaction}}=h^T\mu$ ，细节详见 COMSOL

一般形式

全称：General Form PDE，简称：g

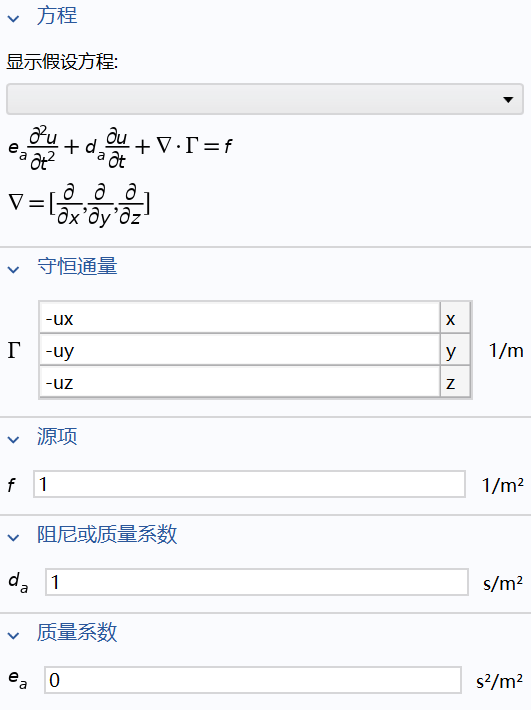
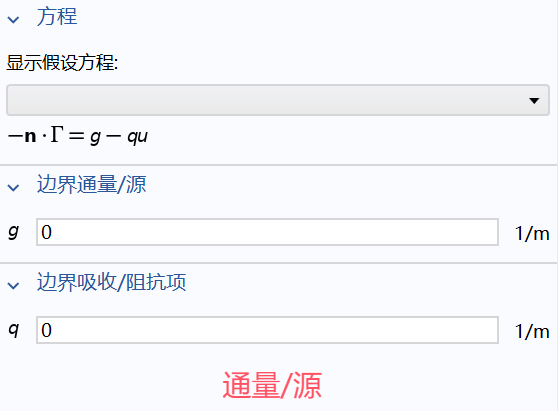
方程：

$$\{\begin{array}{llc}& e_a\frac{{\partial }^{2}u}{\partial t^2}+d_a\frac{\partial u}{\partial t}+\nabla \cdot \Gamma +\beta \cdot \nabla u+au=f,& \mathrm{in}\Omega \\ & -\mathbf{n}\cdot \Gamma =g-qu+h^T\mu ,& \mathrm{on}\partial \Omega \\ & 0=R,& \mathrm{on}\partial {\Omega }_c\\ & u=r,& \mathrm{on}\partial {\Omega }_d\end{array}$$

其中，$\Gamma$ 表示守恒通量

其余和系数形式是一样的

弱形式

上述两种方程称为强形式PDE，它要求解 $u$ 在定义域 $\Omega$ 内具有足够的光滑性（通常是二阶连续可微，记作 $u\in C^2(\Omega )$），并且在每个点都严格满足方程

然而：

1. 实际问题中的解可能不够光滑。例如，在材料界面或有集中载荷的地方，解的导数可能不连续。
2. 在有限元方法中，通常用分段多项式来近似解。这些分段多项式通常只具有较低的连续性（例如，一阶连续），不满足强形式对二阶导数的要求。

弱形式的推导通常通过将强形式PDE乘以一个测试函数 $v$（test function），然后在定义域上积分，并利用分部积分（散度定理）来降低对解 $u$ 的导数阶数

---

以常见的PDE形式 $\nabla \cdot \Gamma =f$ 为例，引入测试函数：

$${\int }_{\Omega }v\nabla \cdot \Gamma \mathrm{d}V={\int }_{\Omega }vf\mathrm{d}V$$

有 $v\nabla \cdot \Gamma =\nabla \cdot (v\Gamma )-(\nabla v)\cdot \Gamma$，得：

$${\int }_{\Omega }v\nabla \cdot \Gamma \mathrm{d}V={\int }_{\Omega }\nabla \cdot (v\Gamma )\mathrm{d}V-{\int }_{\Omega }(\nabla v)\cdot \Gamma \mathrm{d}V={\int }_{\partial \Omega }v(\Gamma \cdot \mathbf{n})\mathrm{d}S-{\int }_{\Omega }(\nabla v)\cdot \Gamma \mathrm{d}V$$

得：

$${\int }_{\partial \Omega }v(\Gamma \cdot \mathbf{n})\mathrm{d}S-{\int }_{\Omega }(\nabla v)\cdot \Gamma \mathrm{d}V={\int }_{\Omega }vf\mathrm{d}V$$

把左边的项全部移到右边去：

$$0=-{\int }_{\partial \Omega }v(\Gamma \cdot \mathbf{n})\mathrm{d}S+{\int }_{\Omega }\left((\nabla v)\cdot \Gamma +vf\right)\mathrm{d}V$$

考虑扩散方程 $\Gamma =-c\nabla u$ ，令 $c=1$，$f=1$，代入上式第二项：

$${\int }_{\Omega }\left((\nabla v)\cdot \Gamma +vf\right)\mathrm{d}V={\int }_{\Omega }\left(-\nabla v\cdot \nabla u+v\right)\mathrm{d}V$$

上式刚好是COMSOL默认的弱表达式（其中test(u)指的是 $u$ 的测试函数）

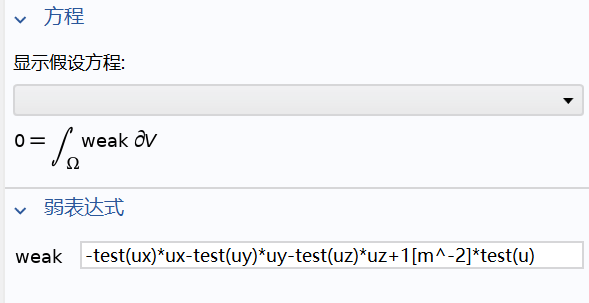
可以看到COMSOL中弱形式只是 $\Omega$ 中方程的积分形式，而边界形式依然是用一般形式的情况来定义的

---

完整的三维空间中的弱形式可以写为：

$$0=\sum _{i=0}^{N_3}{\int }_{{\Omega }_i}{W}_3^i\mathrm{d}{V}_i+\sum _{j=1}^{N_2}{\int }_{\partial {\Omega }_j}{W}_2^j\mathrm{d}{A}_j+\sum _{k=1}^{N_1}{\int }_{{\partial }^2{\Omega }_k}{W}_1^k\mathrm{d}{L}_k+\sum _{m=1}^{N_0}\sum _{m=1}^{N_0}{W}_0^m$$

从左往右分别表示三维域贡献，二位边界贡献，一维线贡献，零维点贡献（${\partial }^3{\Omega }_m$）